PARTS AND MATERIALS
- Calculator (or pencil and paper for doing arithmetic)
- 6 volt battery
- Two 1/4 watt resistors: 10 Ω and 330 Ω.
- Small thermometer
The resistor values need not be exact, but within five percent of the figures specified (+/- 0.5 Ω for the 10 Ω resistor; +/- 16.5 Ω for the 330 Ω resistor). Color codes for 5% tolerance 10 Ω and 330 Ω resistors are as follows: Brown, Black, Black, Gold (10, +/- 5%), and Orange, Orange, Brown, Gold (330, +/- 5%).
Do not use any battery size other than 6 volts for this experiment.
The thermometer should be as small as possible, to facilitate rapid detection of heat produced by the resistor. I recommend a medical thermometer, the type used to take body temperature.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 1, chapter 2: "Ohm's Law"
LEARNING OBJECTIVES
- Voltmeter use
- Ammeter use
- Ohmmeter use
- Use of Joule's Law
- Importance of component power ratings
- Significance of electrically common points
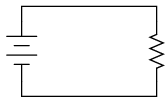
SCHEMATIC DIAGRAM
ILLUSTRATION

INSTRUCTIONS
Measure each resistor's resistance with your ohmmeter, noting the exact values on a piece of paper for later reference.
Connect the 330 Ω resistor to the 6 volt battery using a pair of jumper wires as shown in the illustration. Connect the jumper wires to the resistor terminals before connecting the other ends to the battery. This will ensure your fingers are not touching the resistor when battery power is applied.
You might be wondering why I advise no bodily contact with the powered resistor. This is because it will become hot when powered by the battery. You will use the thermometer to measure the temperature of each resistor when powered.
With the 330 Ω resistor connected to the battery, measure voltage with a voltmeter. In measuring voltage, there is more than one way to obtain a proper reading. Voltage may be measured directly across the battery, or directly across the resistor. Battery voltage is the same as resistor voltage in this circuit, since those two components share the same set of electrically common points: one side of the resistor is directly connected to one side of the battery, and the other side of the resistor is directly connected to the other side of the battery.

All points of contact along the upper wire in the illustration (colored red) are electrically common to each other. All points of contact along the lower wire (colored black) are likewise electrically common to each other. Voltage measured between any point on the upper wire and any point on the lower wire should be the same. Voltage measured between any two common points, however, should be zero.
Using an ammeter, measure current through the circuit. Again, there is no one "correct" way to measure current, so long as the ammeter is placed within the flow-path of electrons through the resistor and not across a source of voltage. To do this, make a break in the circuit, and place the ammeter within that break: connect the two test probes to the two wire or terminal ends left open from the break. One viable option is shown in the following illustration:
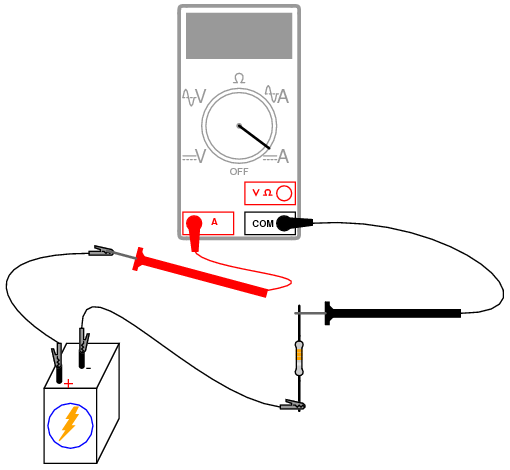
Now that you've measured and recorded resistor resistance, circuit voltage, and circuit current, you are ready to calculate power dissipation. Whereas voltage is the measure of electrical "push" motivating electrons to move through a circuit, and current is the measure of electron flow rate, power is the measure of work-rate: how fast work is being done in the circuit. It takes a certain amount of work to push electrons through a resistance, and power is a description of how rapidly that work is taking place. In mathematical equations, power is symbolized by the letter "P" and measured in the unit of the Watt (W).
Power may be calculated by any one of three equations -- collectively referred to as Joule's Law -- given any two out of three quantities of voltage, current, and resistance:

Try calculating power in this circuit, using the three measured values of voltage, current, and resistance. Any way you calculate it, the power dissipation figure should be roughly the same. Assuming a battery with 6.000 volts and a resistor of exactly 330 Ω, the power dissipation will be 0.1090909 watts, or 109.0909 milli-watts (mW), to use a metric prefix. Since the resistor has a power rating of 1/4 watt (0.25 watts, or 250 mW), it is more than capable of sustaining this level of power dissipation. Because the actual power level is almost half the rated power, the resistor should become noticeably warm but it should not overheat. Touch the thermometer end to the middle of the resistor and see how warm it gets.
The power rating of any electrical component does not tell us how much power it will dissipate, but simply how much power it may dissipate without sustaining damage. If the actual amount of dissipated power exceeds a component's power rating, that component will increase temperature to the point of damage.
To illustrate, disconnect the 330 Ω resistor and replace it with the 10 Ω resistor. Again, avoid touching the resistor once the circuit is complete, as it will heat up rapidly. The safest way to do this is to disconnect one jumper wire from a battery terminal, then disconnect the 330 Ω resistor from the two alligator clips, then connect the 10 Ω resistor between the two clips, and finally reconnect the jumper wire back to the battery terminal.
Caution: keep the 10 Ω resistor away from any flammable materials when it is powered by the battery!
You may not have enough time to take voltage and current measurements before the resistor begins to smoke. At the first sign of distress, disconnect one of the jumper wires from a battery terminal to interrupt circuit current, and give the resistor a few moments to cool down. With power still disconnected, measure the resistor's resistance with an ohmmeter and note any substantial deviation from its original value. If the resistor still measures within +/- 5% of its advertised value (between 9.5 and 10.5 Ω), re-connect the jumper wire and let it smoke a bit more.
What trend do you notice with the resistor's value as it is damaged more and more by overpowering? It is typical of resistors to fail with a greater-than-normal resistance when overheated. This is often a self-protective mode of failure, as an increased resistance results in less current and (generally) less power dissipation, cooling it down again. However, the resistor's normal resistance value will not return if sufficiently damaged.
Performing some Joule's Law calculations for resistor power again, we find that a 10 Ω resistor connected to a 6 volt battery dissipates about 3.6 watts of power, about 14.4 times its rated power dissipation. Little wonder it smokes so quickly after connection to the battery!

No comments:
Post a Comment
Please give valuable comments on this post.